Mandelstam's demonstration of sidebands

Pieter-Tjerk de Boer, PA3FWM web@pa3fwm.nl

(This is an adapted version of an article I wrote for the Dutch amateur radio magazine Electron, July 2021.)

This article describes a simple experiment to show the existence of sidebands, and discusses its history and some theory behind it.

Making sidebands tangible

The pictures show a frequency meter for the power grid. It contains 13 metal "reeds" that can vibrate freely, having resonant frequencies between 47 and 53 Hz. Furthermore, it contains an electromagnet, connected to the mains power. Thus, the reeds are subjected to a magnetic force, varying at the rate of the AC mains frequency. Only the tongue whose resonant frequency matches the mains frequency, will vibrate notably. Here in western Europe, this practically means only the 50 Hz reed will ever vibrate, as the mains frequency is normally kept between 49.8 and 50.2 Hz.

It gets more interesting if we don't connect the 50 Hz directly, but via a telegraph key. If we just press the key and keep it pressed for a while, of course only the 50 Hz reed will vibrate. But if we press and release the key e.g. twice per second, we modulate the 50 Hz signal's amplitude with a 2 Hz square wave. This results in sidebands at 50-2=48 and 50+2=52 Hz. And indeed, then three reeds vibrate, as shown in the next figure.

This simple experiment makes sidebands very visible; almost literally "tangible" via the telegraph key. A picture doesn't really do justice to this, so I've put a movie on YouTube. But the best is to experience it yourself.

If you want to reproduce the experiment, please take note of the following:

1) Safety first; don't connect the 230 V mains directly to the telegraph key! My frequency meter turned out to have a resistor in series with the electromagnet coil, limiting the current to about 2 mA at 230 V. I've replaced this resistor by a much lower value, so now 12 V suffices for the same 2 mA.

2) This experiment requires more voltage on the electromagnet than normal use. The voltage is there only half the time (namely when the key is pressed), so less energy is transferred; and furthermore, that energy is spread over multiple reeds.

3) A telegraph key invites one to send a quick series of morse dots, but that won't work here. E.g., at a morse speed of just 12 words per minute, each dot and each pause lasts 0.1 s, resulting in a 5 Hz squarewave. That would put the sidebands at 45 and 55 Hz, outside the range of the meter. So one should key relatively slowly.

4) Manipulate the telegraph key at a very regular pace, in other words, make sure your modulation frequency is constant. Otherwise, the sidebands are smeared out over multiple reeds and are hardly visible.

5) It seems that in most such frequency meters the reeds actually do not vibrate at 50 Hz but at 100 Hz, despite the scale being labeled as 50 Hz. This is because the metal reeds are attracted by the electromagnet both in the positive and in the negative peaks of the 50 Hz mains sinewave, so 100 times per second in total. My frequency meter seems to be an exception, with the reeds really vibrating at 50 Hz, thanks to an additional permanent magnet which makes the reeds react differently to the positive and negative half of the sinewave.

If your frequency meter has reeds vibrating at the double frequency, the experiment changes a bit, as follows. If we switch a 100 Hz signal on and off 2 times per second, the sidebands end up at 98 and 102 Hz. But the corresponding reeds are labelled as 49 and 51 Hz. Thus, it looks as if the sidebands are half as far away from the carrier than expected.

An old idea

I didn't invent this way of demonstrating sidebands myself. It was invented in the early days of radio by the Russian scientist Leonid Mandelstam (1879-1944). This story is told [2] in the December 1986 issue of the Russian amateur radio magazine Радио (Radio). For your enjoyment, here's a translation of the core of that article:

The presence of sidebands in the spectrum of the radio signal is now, perhaps, known to every radio amateur. But that is now. 70 years ago, when the Russian engineer Mikhail Vasilyevich Shuleikin in his article [7] from 1916 analytically proved the presence of sidebands, experts did not believe him. The discussion about the reality of the existence of sidebands dragged on for several years. Even the famous English scientist John Ambrose Fleming (the inventor of the vacuum diode, a prominent specialist in the field of radiotelegraphy and radiotelephony) categorically denied their existence.

And then the Soviet scientist Leonid Isaakovich Mandelstam assembled a simple circuit from a vibration (reed) frequency meter and a telegraph key and connected it to an alternating current network. When the key was pressed, the frequency meter plate began to oscillate at the number 50. When the key was intermittently closed and opened (during manipulation), neighboring plates began to oscillate - to the right and left of the number 50. During slow manipulation, plates close to the number 50 oscillated, while faster - distant ones.

Fleming was defeated and recognized the reality of sidebands. This experiment, genial in its simplicity, proved the correctness of the analytical conclusions of M.V. Shuleikin - practice had confirmed the theory!

Note the cold-war flavour of the text, emphasizing that the Russians are geniuses and the Englishman is dumb. That flavour may fit the time when this was written (1986), but it doesn't quite fit the truth.

According to [3] already in 1915, that's a year before Shuleikin's article, people in America were thinking about single-sideband transmissions, and even applied for a patent, so sidebands were really already known there at that time. Of course, it is possible that Shuleikin didn't know these American developments and independently came to the same conclusions.

Also the story about Fleming probably is only half true, see below.

But all of that doesn't detract from the experiment's brilliance and simplicity!

(Thanks to Andy RW3DOH for telling me about this experiment and tracking down the 1986 Радио article, and to Google Translate for the basis of the translation.)

Fleming's doubt

It turns out that Fleming was indeed sceptical about the existence of sidebands. As late as January 1930, he published an article [5] in Nature (not the least of scientific journals) in which he argues that sidebands only exist mathematically, and that there's no need to separate radio transmitter frequencies by several kHz because of them. He claims one should just improve the selectivity of the receivers instead.

This is rather surprising. Fleming definitely was a renowned scientist. Furthermore, by that time, 1930, the existence of sidebands was widely accepted. Already since 1927 a transatlantic telephone link was in operation using single-sideband modulation; Fleming must have known about this, being a radio scientist himself and living in the country where the European end of that link was installed.

Anyway, Fleming's article provoked a discussion about the reality of sidebands, first in the "Letters to the Editor" section of Nature, and later in other magazines such as Wireless World. This discussion continued far into 1931, and Fleming's view didn't get much support. But Mandelstam did not participate in this discussion, as far as I've been able to find out.

However, Mandelstam did respond to Fleming's mistake, in his lectures on vibrations given in the years 1930-32, of which reports have been published posthumously [6]. Unfortunately, these reports do not mention any nice demonstrations that he might have used for that. Furthermore, it's unlikely Fleming ever heard of Mandelstam's response: according to [4], no evidence for this can be found in Fleming's publications, nor in his archived correspondence. So the story that Fleming got convinced by Mandelstam's nice demonstration, is probably not true.

How does it work?

Let's reason a bit about those vibrating reeds. We understand that the reeds at 48 and 52 Hz vibrate because someone mathematically calculated that sidebands exist. However, vibrating pieces of metal don't know math. Can we also understand without math why those reeds at 48 and 52 Hz start to vibrate?

Have a look at the next figure, showing a number of signals, and how a resonator (a reed of the frequency meter) responds to that. For clarity, the figure is based on a carrier of 10 Hz rather than 50 Hz, during 4 seconds.

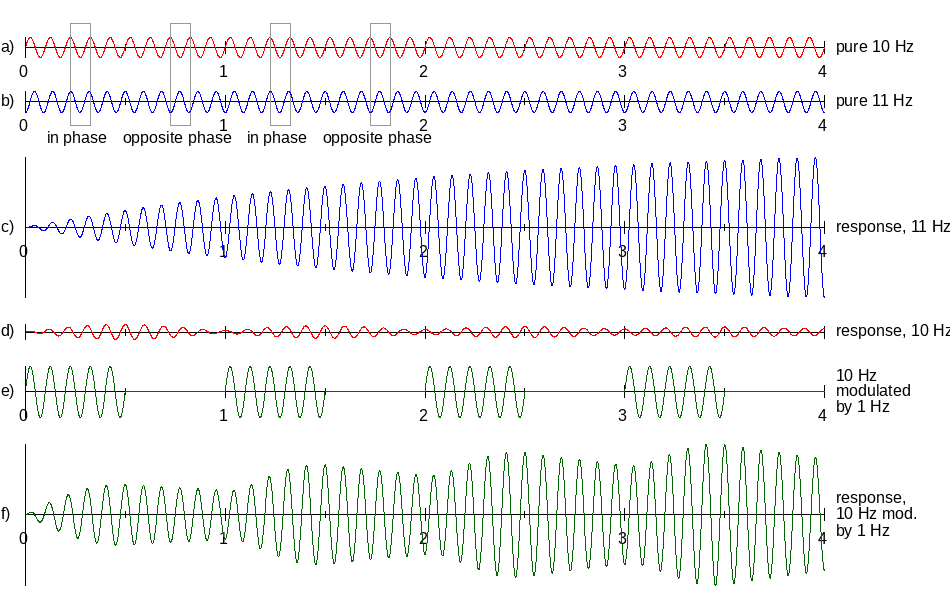Lines (a) and (b) show simple sinewaves of 10 Hz and 11 Hz, respectively. Comparing these, we see that in the course of one second, the sines alternate between being in phase and in opposite phase.

Line (c) shows how an 11 Hz reed reacts to an 11 Hz sinewave: we see it vibrates with an increasing amplitude, although at some point it will not increase further. So if a reed is driven at its own resonant frequency, it takes a while before it vibrates at maximum amplitude. That's also visible in the experiment: after pressing the telegraph key, it takes a few seconds before the 50 Hz reed vibrates maximally.

Line (d) shows how the 11 Hz reed reacts to the 10 Hz sinewave (line (a)). We see that the reed initially starts to move a bit, but in the second half of the first second the amplitude decreases again to (almost) zero. This is because the 10 Hz (driving force) and the 11 Hz (the reed's own frequency) then are in opposite phase (like lines (a) and (b)), so the 10 Hz then counteracts the reed's vibration. All that was achieved during the first half second, is un-done during the second half second. So in contrast to what we saw at (c), the reed's vibration amplitude is not increasing more and more.

Line (e) again shows the 10 Hz signal, but now keyed at 1 Hz, and line (f) shows how the reed reacts to this modulated signal. During the first half second the reed starts to move, like we saw at (d). But while line (d) lost its amplitude during the second half second, that doesn't happen now at line (f). This is because due to the modulation in line (e), the 10 Hz drive is not present during the second half second, so it can't counteract the reed's vibration as it did in (d). The amplitude decreases only a little bit due to losses (friction). In the third half second the 10 Hz signal is present again, and is in phase with our reed's 11 Hz vibration, so the amplitude can increase again. Then follows another half second during which the amplitude decreases only a little bit, and so on. We see that the modulation "removes" precisely those parts of the 10 Hz that would otherwise counteract the 11 Hz. As a consequence, the 11 Hz reed can vibrate increasingly fiercely, similar to line (c) where we applied 11 Hz.

What we actually did here, is reason in the time domain why an 11 Hz reed indeed vibrates when subjected to 10 Hz with 1 Hz modulation. The time domain (what we did here) and the frequency domain (discussing sidebands) are two different but equivalent ways of looking at the same signal. Sometimes one method is handier, sometimes the other.

References

[1] https://youtu.be/YY9q3x5uB1Y
[2] В. Крыжановский: Из истории радиотехники: можно ли увидеть боковые частоты? Радио, 12/1986, p. 38-39.
(in Russian. V. Kryzhanovsky: From the history of radio technology: is it possible to see sidebands?)
Available online at https://radiojournal.ru/radio-1986-god/
[3] Arthur A. Oswald: Early History of Single-Sideband Transmission. Proc. IRE, 1956. (available online at IEEE)
[4] Alexander Pechenkin: L.I. Mandelstam and his school in physics, 2019.
[5] Sir Ambrose Fleming: The `Wave Band' Theory of Wireless Transmission. Nature, January 18, 1930.
https://www.nature.com/articles/125092a0
[6] Л.И. Мандельштам. Полное собрание трудов. IV. Лекции по колебаниям (1930-1932). 1955.
(in Russian; L.I. Mandelstam: Collected works, part IV. Lectures on oscillations.)
Available online at http://alexandr4784.narod.ru/mandelcshtam.html
[7] Михаил Васильевич Шулейкин: "Об условиях применения генераторов высокой частоты в радиотелефонии". Известия по минному делу, 1916, No. 49, pp. 1-15.
(in Russian; Mikhail Vasilyevich Shuleikin: "On the conditions for the use of high-frequency generators in radiotelephony")
(If you have access to this article, I'd much appreciate getting a copy!)